R
ich Ciapala did a great, extensive review of Windows Compute Cluster Server 2003 in the April, 2006 edition of MSDN Magazine. He took a sample application (matrix multiplication) and runs it on CCS three different ways: in a single call, as a distributed application using several calls, and as a single, MPI-enabled application.It's a great, in-depth article. Rich dove in headfirst, and he dove in deep! Thanks for such a practical, hands-on guide. Matrix multiplication takes a ton of calculation to do and is very parallelizable, so it's a great sample.
In fact, it was such a good sample, I decided to take the same application and implement it using the Digipede Network!
We don't have an MPI implementation (and if you need it, CCS is the right tool for you!), so I'm going to mimic the functionality of Rich's second example: taking their (command line) matrix multiplication tool, and run it using the Digipede Workbench.
First, I created a 5000 row by 5000 column matrix. For my test, I'm going to write code to square it (multiply it by itself). Each of the 25,000,000 cells in the resulting matrix takes 5000 multiplications to calculate.
Next, in order to have a "control" for my experiment, I multiplied it by itself on one machine. I chose one of our faster servers for this: a 3GHz box. Multiplying my huge matrix by itself on that one machine took just over an hour:

Ok, now we've got a baseline. Next, I used our GUI tool, Digipede Workbench, to create a job submission. The MatrixMultiplier takes the following arguments:
MatrixMultiplier.exe [input matrix] [input matrix] [output matrix] [quadrant X] [quadrant Y] [quadrant dim]For my test, I broke the multiplication up into 16 tasks. For example, the command lines for my first three tasks need to look like this:
MatrixMultiplier.exe InputMatrix.mtx InputMatrix.mtx output0.mtx 0 0 1250
MatrixMultiplier.exe InputMatrix.mtx InputMatrix.mtx output1.mtx 1250 0 1250
MatrixMultiplier.exe InputMatrix.mtx InputMatrix.mtx output1.mtx 2500 0 1250Fortunately, creating command lines like that are a breeze with the Workbench. I did this whole thing using variables, by the way, so I could re-use it later for more matrix multiplication jobs without going through the whole process again.
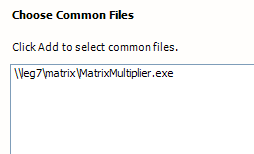
First, I gave it the name of the executable:
Then, I gave it the name of the Matrix I was going to multiply.
I defined XQuadrant as a range variable from 0 to 4999 (the size of my matrix), step 1250.
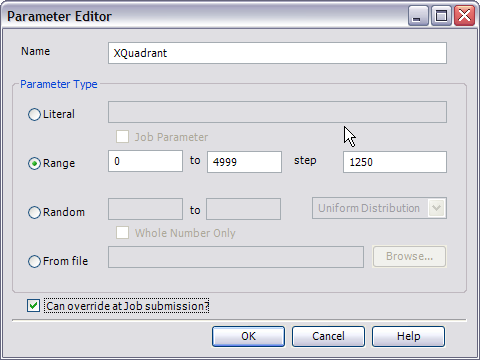
I defined YQuadrant the same way. Then I defined QuadrantSize to be 1250. If, in the future, I want to use this Job to multiply different size matrices (or using different size quadrants), I can change these values on submission.
After telling it where to put the result file, I defined the command line:
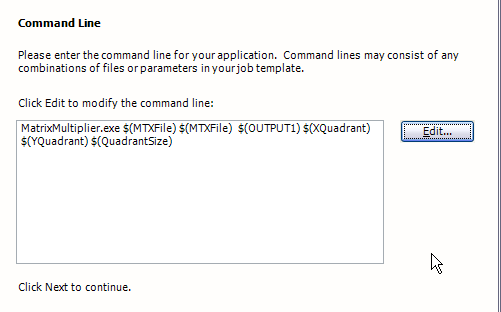
Notice all of the variables on the command-line: the file name of the input file (used twice), the output file name, the quadrants (x and y), and the quadrant size.
Then I clicked "Submit!"
The whole job definition process took about 10 minutes or so. And the job took 13.5 minutes to run--nearly a 4.5x speedup!
Here's an aside: With about 10 machines on the network, I wondered why I was only seeing less than a 5x speedup. I looked at the task times, and I realized that my five slowest machines were so much slower than the others that they were actually holding things up. I resubmitted my job; this time, I broke it into 64 pieces (this was really easy; I just had to go through the wizard again, changing my quadrant size and step sizes to 625. Piece of cake!)
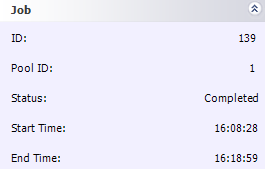
And the results were good: it knocked 3 minutes off my run time, bringing it down to 10.5 minutes. By giving finer-grained work to the Digipede Network, I allowed its CPU load balancing to work most efficiently. My grid did 60 minutes of work in 10 minutes; that's a 6x speedup. Considering that I have 4 fast machines and 5 slow machines (much slower than my "control" machine), the 6x speedup was just about optimal for this problem.
[Update 2007-10-17]: We're doing some testing right now, and we've just added two eight-way boxes to our test grid; today it is 14 machines with a total of 35 cores. I just re-ran this test and it took two minutes and 19 seconds. Yum!
Matrix multiplication should be easy to parallelise, but it's a whole new game when you talk about matrix inversion, and probably other useful matrix operations such as a Cholesky decomposition. Here's a link to an example of matrix operations over multiple computers not working to plan!
ReplyDeletehttp://www.vislab.uq.edu.au/research/gridmathematica/gridmathematica.html
Yep - not every problem can be broken up at all; some things just run on one machine. And, almost always, problems can't necessarily be broken up into zillions of pieces. As you continue to break the problem up into smaller pieces, you incur more overhead--if your problem isn't "big" enough, there's no reason to break it into smaller pieces. The other added consideration is bandwidth. In the example cited in that page, there is considerable communication between the nodes, so increasing the number of nodes increased traffic (and eventually swamped the network). As you can read in a recent post of mine, sometimes problems are only distributable on a higher bandwidth connection.
ReplyDeleteThe lesson from both of these issues is that distributed computing is not a panacea for "make everything run faster." It has certain applications for which it is perfect; it has many other applications for which it is a great (but perhaps not quite perfect) tool. And there are still other applications for which it doesn't yet make sense.